Paradokser i fysik Kaos i solsystemet? Til denne del hører et program, "Kloder". Download zip-fil: Kloder001121.zip Udpak zip-fil (bevar mappe-struktur!), læs vejledningerne og kør programmerne KloderN.EXE eller Kloder3.EXE		Illustration fra: "Planeter", Kaare Lund Rasmussen og Torsten Meyer, Munksgaards Dimensioner, 1998. En del af den følgende tekst samt nogle af billederne er hentet fra samme kilde.

Determinisme: den mekaniske vision og Laplace's dæmon

Den newtonske mekanik, med Newtons tre love og gravitationsloven, giver en deterministisk beskrivelse af naturen. At en række af hændelser er deterministiske betyder, at kendskab til systemets tilstand på et givet tidspunkt fører til, at alle senere tilstande for systemet er forudbestemte.

Programmet 'KloderN' kan udføre simulationer af N kloders indbyrdes bevægelser, hvor N er et valgt antal kloder, som alle påvirker hinanden.

Mere om Newton's love og anvendte enheder i programmerne 'Kloder'

KloderN.exe model KLN.003
- Stjerne med planet (planet-masse = 0, så planeten ikke påvirker stjernen)
- Indlæs modellen, menu 5-1, kln.003
- (benyt Enter flere gange for at komme videre, f.eks. tilbage til hovedmenuen)
- Vælg forsinkelse: menu 3-5-3, sinke=1000
- Skift evt. til "klodevisning": menu 3-2-1 (flag fmrk=1)
- Kør simulering, menu 1

Stjernens kræfter på planeten er givet ved Newton's gravitationslov.
Kendes på et bestemt tidspunkt planetens position og hastighed (både størrelse og retning) kan planetens position og hastighed beregnes i al fremtid (og al fortid) ved brug af Newton's 2. lov.
Planetens bevægelse er deterministisk - og den er også reversibel, dvs. planetens bevægelse er fysisk mulig og korrekt også hvis "filmen" køres baglæns.

KloderN.exe model KLN.003
- Skift fortegn for planetens hastighed (klode 2), menu 2-2, klode 2, vx uændret, vy=-5.443

Den store succes, som Newtons mekanik fik, frembragte en tro på, at alle fænomener i naturen ville kunne beskrives deterministisk. Denne tanke blev rendyrket af den franske matematiker og filosof Pierre-Simon de Laplace (1749-1827). Han udtrykte sin vision om den mekaniske fysiks muligheder ved en tænkt fremtoning, som senere er blevet døbt "Laplace's dæmon". Denne dæmon antages på et givet tidspunkt at kende til alle tilstande og kræfter i universet. Han kan så beregne sig frem til alle fremtidige tilstande (og tilbage til alle tidligere). Såvel fortiden som fremtiden vil således være fastlagt og kendt af dæmonen.

Denne holdning, at den mekaniske fysik efterhånden skulle kunne give os en deterministisk beskrivelse af hele verden, har haft stor betydning i videnskabens udvikling. Ikke kun i fysik og kemi, men også i andre videnskaber som for eksempel biologi, medicin - og endda sociologi og psykologi. Tanken indgår også i dag i mange menneskers syn på videnskabens muligheder. Men der er også en øget kritisk holdning mod ideen.

Hvis vi holder os inden for den mekaniske fysiks reversible processer, kan determinismen imidlertid ikke betvivles.

Prøv også:

KloderN.exe model KLN.004
- Stjerne med tung planet (planeten påvirker stjernen)

KloderN.exe model KLN.001
- Dobbeltstjerner med masseløse planeter

KloderN.exe model KLN.002 eller KLN.A02
- Tre planeters dans

KloderN.exe model KLN.005
- Stjerne med 2 tunge planeter

KloderN.exe model KLN.006
- Sol, planet og måne

KloderN.exe model KLN.007 eller KLN.A07
- Vær en gud, 7 planeter
- Rafle: menu 6-4

Det sidste eksempel - at agere en gud - viser hvor svært det er at lave et stabilt system.

Kaos i solsystemet? - En prisopgave om stabilitet

For at fejre Kong Oscar II af Sverige og Norge (1829-1907) på hans 60-års fødselsdag foreslog en svenske matematik-professor, at der skulle udskrives en konkurrence om den bedste videnskabelige prisopgave til aflevering den 21. januar 1889. Et af de problemer, som man ønskede løst, var følgende:

"For et system bestående af vilkårligt mange masse-partikler, som tiltrækker hinanden ifølge Newtons love, og under antagelse af, at intet par af partikler kolliderer, ønskes en fremstilling af partiklernes koordinater til alle tider, udtrykt som en sum af konvergente serier, hvis led består af kendte funktioner"

I lidt mere almindeligt sprog kan det oversættes til: Eftervis matematisk, at Solsystemet udvikling kan beskrives i al fremtid og undersøg herved, om Solsystemet er stabilt. Matematisk set handler det om løsninger til de såkaldte differentialligninger.
Vinderen af prisopgaven blev den franske matematiker Henri Poincaré (1854-1912). Han satte sig for at undersøge en fremherskende antagelse om matematikken bag gravitation mellem flere legemer: nemlig at en lille ændring i nogle af de størrelser, som indgår i ligningerne kun medfører små forskelle i løsningerne. Er dette tilfældet, er der god grund til at tro, at Solsystemet er stabilt.
Mere præcist formuleret: Man tager en model for et antal planeter og vælger et sæt start-værdier. Så følger man bevægelserne 10 år frem i tiden og aflæser derefter x-koordinaten for et bestemt legeme. Regne-eksperimentet gentages, men med en ændring i startværdi for det udvalgte legemes x-koordinat på 1%. Vil legemets x-koordinat efter de 10 år med den nye startværdi afvige meget eller kun lidt fra den første placering?

Problemet hænger sammen med spørgsmålet om, hvorvidt løsninger til Newtons ligninger kan beskrives med kendte "pæne" funktioner. En planet i et fast gravitationsfelt, for eksempel dannet af en tung sol, eller to stjerner i indbyrdes vekselvirkning, kan beskrives matematisk "pænt". Men allerede ved inkorporeringen af tre legemer opstår der problemer. Newton var selv opmærksom på dette. Hans forsøg på at give en tilnærmet beskrivelse af Månens bevægelser og vekselvirkning med Jorden under indflydelse af gravitationsfeltet fra Solen førte ikke til noget tilfredsstillende resultat. I tiden efter Newton blev dette såkaldte tre-legemeproblem en udfordring for både fysikere og matematikere.
Man antog, at selv om tre-legemeproblemet var uløseligt i traditionel forstand, så kunne man opstille tilnærmede løsninger med vilkårlig stor nøjagtighed. Poincaré var den første der såede tvivl om dette. Han påviste ved specielle matematiske teknikker, at tre eller flere legemer kan have deterministisk kaotisk adfærd. Denne betegnelse er dog ikke Poincaré's egen, men er kommet til i vor tid, hvor mange af Poincaré's forudsigelser er blevet bekræftet og gjort synlige ved hjælp af regnemaskiner. Med Poincaré's ord fra 1903 (oversat fra en engelsk oversættelse i Ivars Peterson: "Newton's Clock"):

"En meget lille årsag, der helt undslipper vores opmærksomhed, kan forårsage en betragtelig effekt, som vi på ingen måde kan overse, og vi siger da, at denne effekt skyldes tilfældighederne. Hvis vi kendte de helt præcise naturlove og alle tilstande i universet i startøjeblikket, så kunne vi forudsige universets tilstand præcist i et givet øjeblik derefter. Men selvom det var tilfældet, at naturlovene ikke længere gemte nogen hemmeligheder for os, kunne vi stadig kun tilnærmelsesvist kende begyndelsestilstanden. Hvis dette tillod os at bestemme den efterfølgende tilstand med den samme tilnærmelse, så ville det være alt, vi kunne forlange, og vi ville sige, at fænomenet var forudsagt, at det bliver styret af naturlovene. Men det er ikke altid således; det kan ske, at små forskelle i begyndelsestilstanden producerer meget store forskelle i sluttilstanden. En lille fejl i begyndelsestilstanden vil herved producere en enorm fejl i sluttilstanden. Forudsigelse bliver umulig, og vi har et tilfældigt fænomen."

Den omtalte overfølsomhed over for begyndelsesbetingelserne ligger til grund for den moderne definition på deterministisk kaos. Som et berømt eksempel kan nævnes, at vejr-situationen i Danmark, der er stærkt kaotisk over et tidsrum på nogle uger, kan tænkes påvirket af, hvorvidt en sommerfugl i Sydamerika blafrer med vingerne eller ej.
Men hvis forudsigelser langt frem i tiden er umulige på grund af stor følsomhed i begyndelsesbetingelserne, så er det heller ikke muligt at give et sikkert udsagn om Solsystemets stabilitet.

Så det er ikke trivielt at svare på spørgsmålet om, hvorvidt Solsystemet er kaotisk eller ej. Først inden for de seneste år har forskerne opnået en viden, så man kan sige, at Solsystemet er kaotisk, men på en stabil eller pæn måde. Der findes direkte kaotiske baner i Solsystemet, for eksempel Saturn-månen Hyperions bane, eller flere af asteroidebanerne, men de er kun kaotiske inden for ganske bestemte rammer (radius-intervaller), og langt de fleste baner i Solsystemet er stabile og forudsigelige langt ud i fremtiden.

For at kunne undersøge kaotiske tilstande for tre legemer nøjere benyttes programmet 'Kloder3'.
'Kloder3' kan i modsætning til 'KloderN' kun behandle tre kloder. Til gengæld har 'Kloder3' en særlig facilitet, idet brugeren kan vælge at benytte et særligt relativt koordinatsystem, som gør det lettere at iagttage bestemte typer kaotiske bevægelser.
I det relative koordinatsystem sker der følgende (se figur):
Klode 1:bevarer sin oprindelige start-x-koordinat, x1, mens y-koordinaten, y1, sættes til nul.
Klode 2:placeres til højre for klode 1 på x-aksen og i den afstand fra klode 1, som i øjeblikket er aktuel.
Klode 3:vises i en position, som er korrekt i forhold til klode 1 og klode 2.

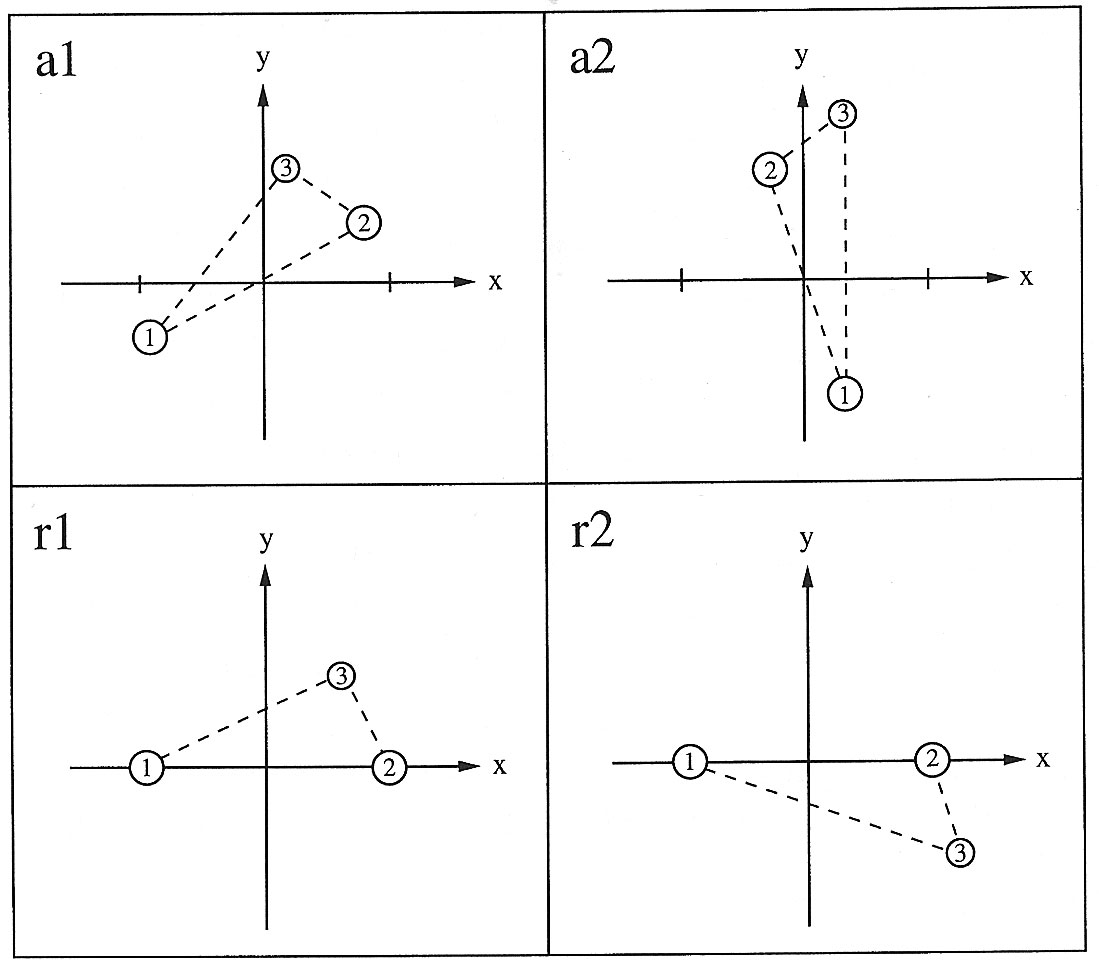
Figurens a1 og a2 viser situationen i det sædvanlige koordinatsystem til to forskellige tider. r1 og r2 viser de samme situationer i det relative koordinatsystem.

Kloder3.exe model KLN.000
- I programmets basisdata (fås ved opstart eller kan hentes ind fra data-filen kl3.000) er klode 1 og 2 stjerner med masser=1, som er sat i cirkulær rotation om deres fælles massemidtpunkt. Klode 3 er en masseløs planet.
- Vælg forsinkelse: menu 3-4-3, sinke=1000
- Skift evt. til "klodevisning" også for klode 3: menu 3-1-3 (flag fmrk3=1)
- Kør simulering, menu 1
- Skift til relativt koordinatsystem, menu: 3-1-4 (flag fksrel=1) og se simulering

Kloder3.exe model KLN.001, KLN.002, KLN.003, KLN.A03, --- ,KLN.D03
- Disse modeller bør køres med:
- sinke=500, menu 3-4-3
- relativt koordinatsystem, menu 3-1-4 (flag fksrel=1)
- Klodevisning for klode 3 fra eller til, menu 3-1-3 (flag mrk3=0 el. 1)
- Vurder hvilke simuleringer der ser forudsigelige ud, og hvilke der ikke gør det (er kaotiske).
- Bemærk i KLN.?003 forskelle i startbetingelserne for klode 3 (position x og hastighed y) (disse kan ses i menu 2) og bemærk forskelle i simuleringsforløbene.
- Lav evt. selv små variationer i startbetingelserne, menu 2-1 og 2-2 og sammenlign simuleringsforløbene.

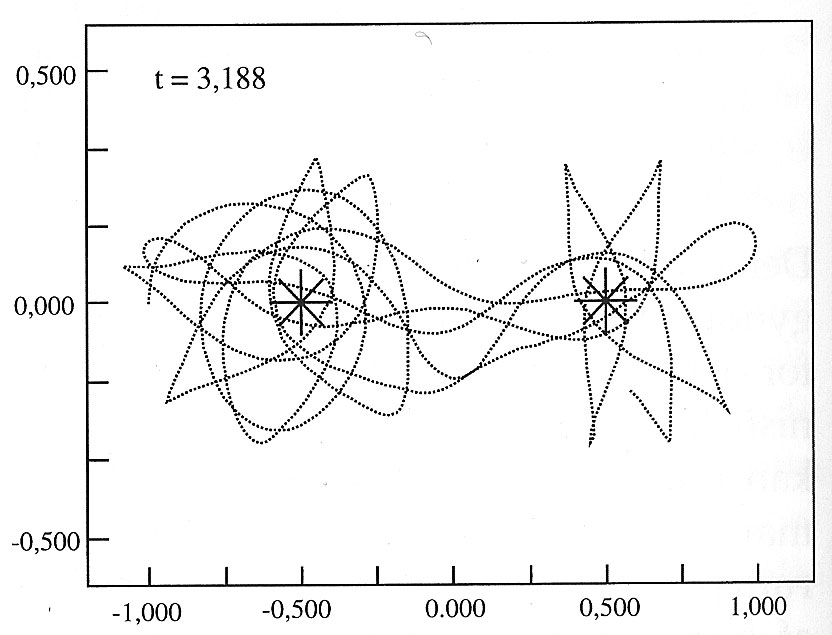
Eksempel på skærmbillede fra programmet 'Kloder3' med simulering af en masseløs planet omkring to stjerner på hever 1 solmasse. Akserne er angivet i AU. Starten på simuleringen er til venstre, slutningen til højre.

Som nævnt havde Newton havde store problemer med at få hold på Månens bevægelser. Alle 'tre-legemeproblemer (her sol - jord - måne) har potentiel kaotisk adfærd.

Kloder3.exe model KLN.004, KLN.005 og KLN.006
- Disse programmer simulerer mere eller mindre realistiske modeller for systemet sol - jord - måne.

Litteratur:

Ivars Peterson: "Newton's Clock - Chaos in the Solar System", W.H.Freeman and Co., 1993.

Kaare Lund Rasmussen og Torsten Meyer: "Planeter", Munksgaards Dimensioner, 1998.

Se mere om: Newton's love og anvendte enheder i programmerne 'Kloder'
Se mere om: Solsystemet som evighedsmaskine
Se mere om: Andre kaos-fænomener